HELLO HOTKEY

안녕하세요, HELLO HOTKEY입니다.

지난 포스팅에서 소개드린 메타코드M '머신러닝 입문 부트캠프' 강의에서 첫번째 챕터인 회귀를 공부한 내용을 공유드리겠습니다.

회귀와 분류

회귀와 분류는 머신러닝에서 가장 기본적이고 중요한 개념입니다. 두 가지 모두 입력값으로 연속값과 이산값을 받을 수 있지만, 출력값의 형태에 따라 구분됩니다. 회귀는 연속적인 값을 출력하고, 분류는 이산적인 값을 출력합니다. 예를 들어, 주택 가격을 예측하는 문제는 회귀 문제이고, 이메일이 스팸인지 아닌지를 분류하는 문제는 분류 문제입니다. 분류 문제에서 출력값이 2개인 경우를 이진분류, 2개 이상인 경우를 다중분류라고 합니다.

회귀와 분류의 수학적 배경

회귀 분석은 종속 변수 Y와 한 개 이상의 독립 변수 X 간의 관계를 찾는 것이 목표입니다. 선형 회귀 모델에서는 Y = β0 + β1X1 + β2X2 + ... + βnXn + ε의 형태로 나타내며, 여기서 β는 회귀 계수, ε는 오차입니다. 분류 문제에서는 데이터 포인트가 특정 클래스에 속할 확률을 예측하기 위해 로지스틱 회귀, 나이브 베이즈, 서포트 벡터 머신(SVM) 등 다양한 알고리즘을 사용합니다.

데이터 셋과 학습 방식

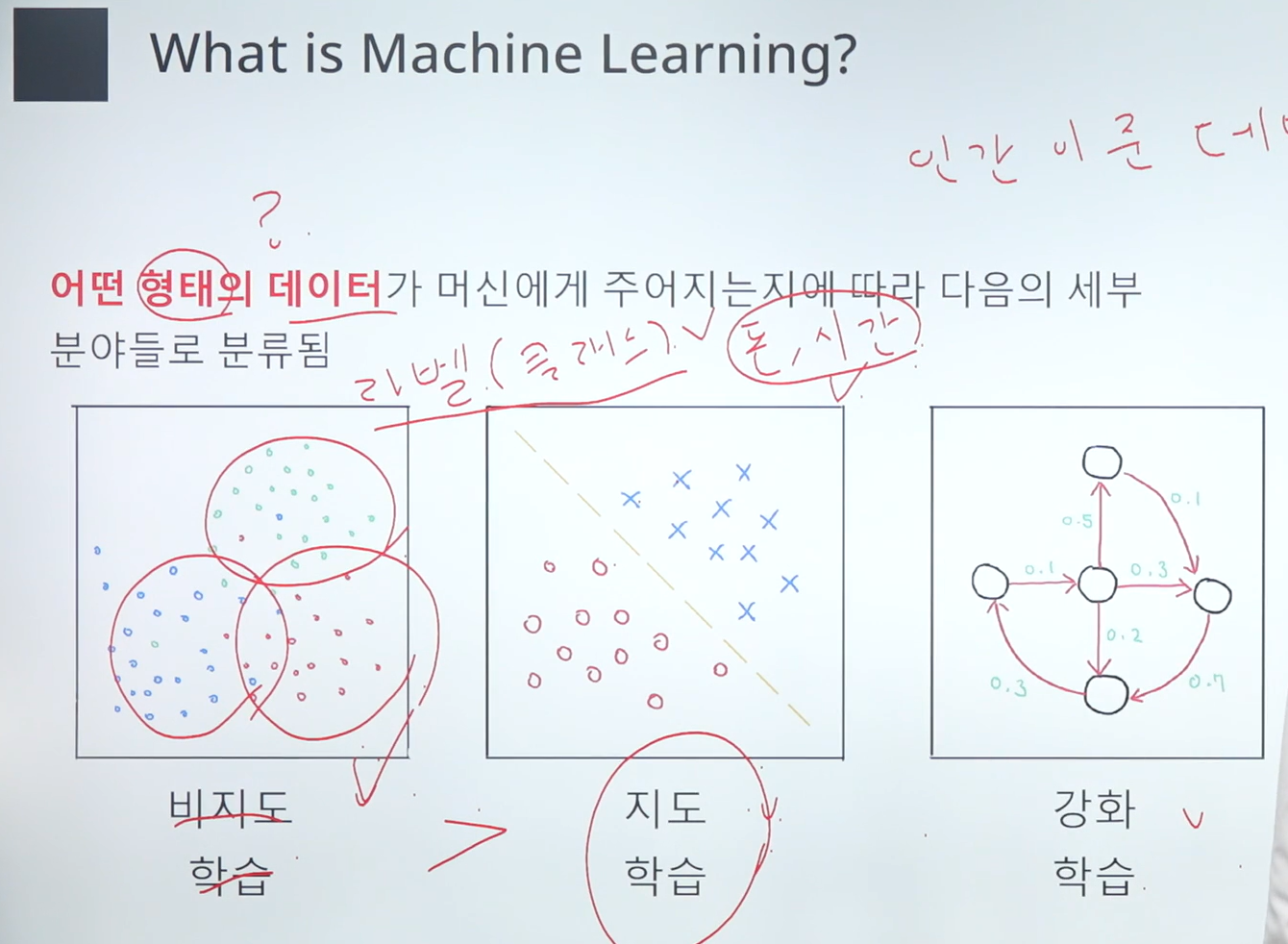
데이터 셋은 독립변수(피쳐)와 종속변수(라벨)로 구성되어 있습니다. 종속변수의 유무에 따라 지도학습과 비지도학습으로 구분됩니다. 파라미터는 모델이 학습을 통해 최적의 결과를 도출하기 위해 조정하는 가중치이며, 하이퍼파라미터는 모델의 구조나 학습 과정에서 연구자가 설정하는 변수입니다.

지도학습과 비지도학습

지도학습(Supervised Learning)은 라벨이 있는 데이터를 사용하여 모델을 학습시킵니다. 예를 들어, 이미지에 대한 캡션을 생성하거나, 텍스트 분류 문제 등이 있습니다. 비지도학습(Unsupervised Learning)은 라벨이 없는 데이터를 사용하여 데이터의 구조를 학습합니다. 클러스터링 알고리즘인 K-means, PCA(주성분 분석) 등이 대표적입니다.

손실 함수와 경사 하강법

머신러닝의 목표는 손실함수를 최소화하는 파라미터를 찾는 것입니다. 손실함수는 모델의 예측값과 실제값 사이의 차이를 나타내며, 평균제곱오차(MSE)나 최소제곱법을 통해 구할 수 있습니다. 복잡한 함수의 경우 경사하강법(Gradient Descent)을 통해 손실함수를 최소화시키는 방향으로 파라미터를 업데이트 합니다.

경사 하강법의 변형

경사 하강법의 기본 원리는 손실함수의 기울기를 이용해 파라미터를 업데이트하는 것입니다. 학습률(learning rate)은 파라미터 업데이트의 크기를 결정하며, 학습 초기에 큰 값을, 학습 후반에는 작은 값을 사용하는 것이 일반적입니다. 이를 위해 스케줄러(scheduler)를 사용하기도 합니다. 예를 들어, Multi-step Scheduler는 학습률을 단계적으로 감소시키고, Cosine Annealing Scheduler는 코사인 함수를 이용해 학습률을 조절합니다.

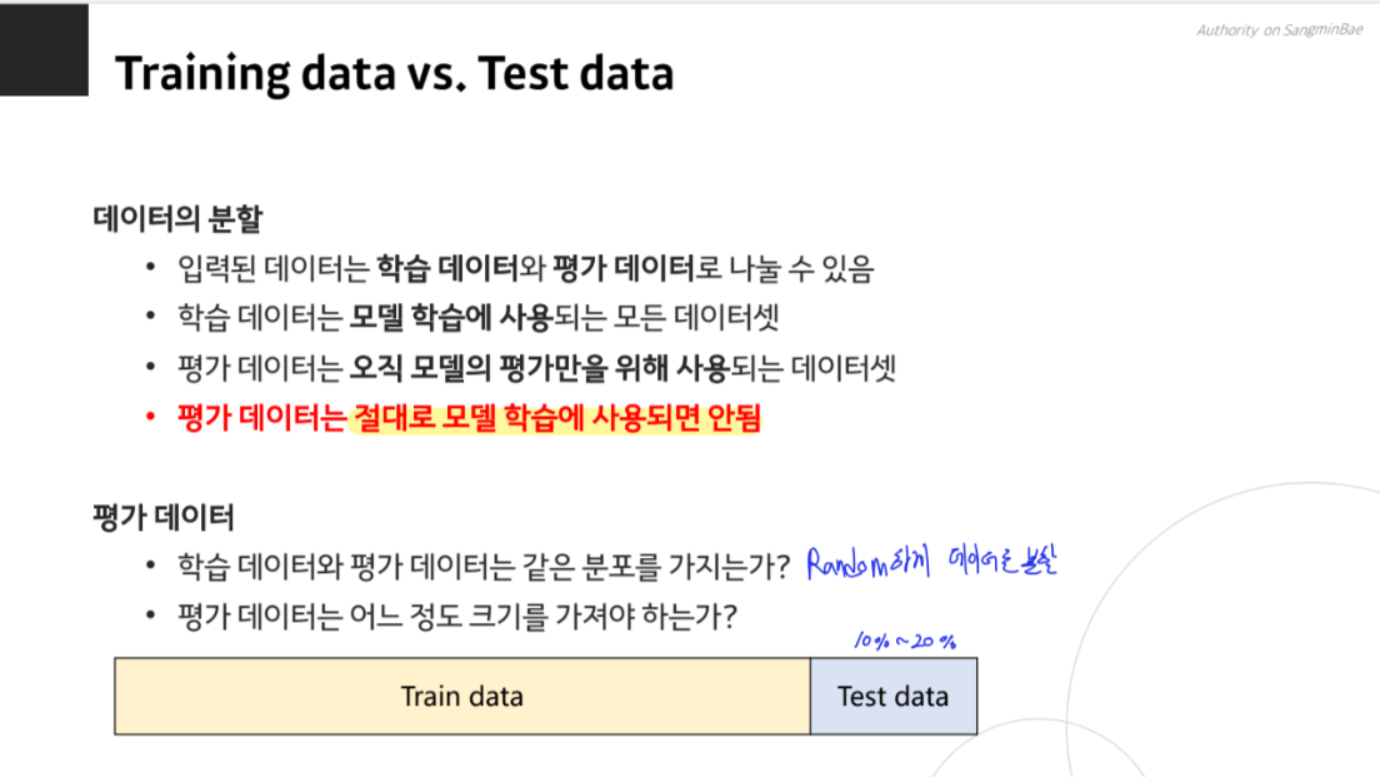
데이터 분할과 교차 검증

데이터를 학습시켜 활용하기 위해서는 Train data, Validation data, Test data로 분할해야 합니다. Validation data는 모델의 성능을 중간에 확인하기 위해 사용하며, Test data는 최종 성능 평가에 사용됩니다. 교차 검증(cross-validation)은 데이터를 여러 번 나누어 모델을 평가하는 방법으로, K-fold 교차 검증은 데이터를 K개로 나누어 K번의 학습과 검증을 수행합니다.

교차 검증의 중요성

교차 검증은 모델의 일반화 성능을 평가하는 데 매우 유용합니다. 단일 Train/Test 분할 방식은 데이터의 분포에 따라 성능이 크게 달라질 수 있으므로, K-fold 교차 검증을 통해 모델의 안정성을 평가할 수 있습니다. 일반적으로 K값이 클수록 더 많은 학습 데이터로 인해 모델이 더 잘 일반화될 수 있지만, 계산 비용이 증가합니다.

정규화와 모델의 복잡성

모델의 복잡성이 커질수록 과적합(Overfitting) 문제가 발생할 수 있습니다. 이를 극복하기 위해 정규화 기법을 사용합니다. Ridge Regression(L2)과 Lasso Regression(L1)은 대표적인 정규화 방법입니다. Ridge Regression은 파라미터의 제곱 합을 최소화하며, Lasso Regression은 파라미터의 절댓값 합을 최소화하여 필요 없는 파라미터를 0으로 만듭니다.

강의를 통해 기본적인 회귀에 대한 이해를 할 수 있었습니다.
다음 포스팅에서는 분류에 대한 내용도 다뤄보겠습니다.
감사합니다!

해당 강의는 서포터즈 지원을 받아 작성하였습니다.

안녕하세요, HELLO HOTKEY입니다.

저는 올해 초 인공지능 대학원에 입학하여 AI 관련 과목들을 공부하고 있습니다. 통계학 중심의 커리큘럼을 따라가다 보니 수학과 통계에 대한 이해가 부족하다고 느꼈습니다. 이에 대학원 강의를 보다 잘 이해하기 위해 필요한 강의를 찾던 중, 드디어 제가 원하는 강의를 발견했습니다. 앞으로 이 강의를 통해 부족한 지식을 채워보고자 합니다.

제가 선택한 강의는 메타코드M에서 제공하는 ‘머신러닝 입문 부트캠프’입니다.
※ 참고로 메타코드M은 데이터 분석에 특화된 온라인 강의 플랫폼으로, 빅데이터 자격증, 데이터 분석, 인공지능 강의와 현직자의 특강을 제공하며, 커리어 방향 설계에 도움을 줍니다.

이 강의는 핵심 기초 이론 설명을 시작으로 매 챕터마다 실습 과정을 포함하여 머신러닝의 동작 원리를 이해하는 데 도움을 줍니다. 강사님은 KAIST 김재철 AI 대학원 박사과정에 재학 중이며 국내 대기업 인공지능 출강 경험도 있습니다.

제가 ‘머신러닝 입문 부트캠프’를 선택한 이유는 회귀(Regression)와 분류(Classification)에 대한 기초적인 지식을 얻기 위함입니다. 대학원에서 다루는 회귀와 분류는 생각보다 복잡하게 설명되어 있어 이해가 부족한 부분을 보완하고자 했습니다. 또한, 이 강의는 회귀와 분류뿐만 아니라 차원 축소, 클러스터링도 다루고 있어 전반적인 머신러닝 동작 원리를 이해하는 데 큰 도움이 될 것이라고 생각했습니다.

이제부터는 강의를 보며 정리한 내용입니다.

챕터 0: Orientation - 인사/강좌소개

• 포함관계: 인공지능(AI) > 머신러닝(ML) > 딥러닝(DL)
• ML과 DL의 차이: 머신러닝은 ‘통계적 모델’을, 딥러닝은 ‘신경망 모델’을 활용
• 머신러닝의 목적: 통계적인 방법 또는 경사하강법을 이용하여 데이터를 잘 표현하는 함수를 찾는 것

데이터 형태에 따른 머신러닝 기법:

• 비지도 학습: 라벨 데이터가 없고 데이터의 특성만 있는 경우 사용
• 지도 학습: 라벨 데이터가 있지만 돈/시간이 많이 소요
• 강화 학습: State(상태)와 Reward(보상) 데이터가 있음 (예: 알파고, ChatGPT, 이미지 생성 모델 등)

• 경사하강법과 고유값/고유벡터 이해의 중요성: 추후 딥러닝 모델 이해에 도움
• 딥러닝의 특징: 신경망 모델을 사용하고 데이터 양이 머신러닝에 비해 많음
• 결론: 빅데이터 시대에서 딥러닝 모델로 나아갈 때 머신러닝 이해는 필수적

이상으로 챕터 0에 대한 소개를 마치겠습니다.
아래 링크를 클릭하시면 강의 상세페이지를 확인하실 수 있습니다.

강의 상세페이지 바로가기

제 글을 읽어주셔서 감사합니다.

강의를 통해 머신러닝에 대한 기초 지식을 탄탄히 다지시길 바랍니다. 감사합니다!

해당 강의는 서포터즈 지원을 받아 작성하였습니다.